If a Rational Function Is Proper Then
Qx and rx can be computed using polynomial division of fxbygx. A rational function is any function which can be written as the ratio of two polynomial functions where the denominator is not 0 0.
The Rational Function Proper And Improper Fractions
However there is a nice fact about rational functions that we can use here.
. Rx Mx R 1 x. A rational function is a function that can be written as the quotient of two polynomial functions. In other words to determine if a rational function is ever zero all that we need to do.
Domain restrictions of a rational function can be. A rational function which is not proper is improperIffxgx is improper then there are polynomials qx and rx such that fxgxqxrxgx where rxgx is a proper rational function. A rational function is any function which can be written as the ratio of two polynomial functions where the polynomial in the denominator is not equal to zero.
It is unclear or not useful. As X gets very big in the positive direction or ex gets very small in the negative direction will get closer and closer to a Y. Every rational function has either a vertical or a horizontal asymptote.
For a rational function R if the degree of the numerator is less than the degree of the denominator then R is Proper The graph of a rational function may intersect a. The rational function fx Px Qx in lowest terms has an oblique asymptote if the degree of the numerator Px is exactly one greater than the degree of the denominator Qx. The domain of f x P x Qx f x P x Q x is the set of all points x x for which the denominator Qx Q x is not zero.
In the first example the numerator is a second-degree polynomial and the denominator is a third-degree polynomial so the rational is proper. Profo Recall that if you divide a polynomial by a divisor then. Px and Qx are polynomials and.
If on the other hand n m then Rx may be represented as a sum of a polynomial Mx of degree η - m and a proper rational function R 1 x P 1 xQx. We have a rational fractions. If Rx pxqx is a rational function and if p and q have no common factors then R is in lowest terms.
If a rational function is proper then _____ is a horizontal asymptote. Is it true that f is a rational function ie. F x x2 5x6 f x x 2 - 5 x 6 is a.
The degree of Px is less than the degree of Qx. Solving an Applied Problem Involving a Rational Function. Show activity on this post.
The basic characteristic of the partial fraction expansion is that X z must be a proper rational function or that the degree of the numerator polynomial N z be smaller than the degree of the denominator polynomial D z assuming both N z and D z are polynomials in either z-1 or z. Proper rational functions A proper rational function is one in which the degree of the numerator is less than the degree of the denominator. So we have some type of all set up that we have a polynomial on top and polynomial on the bottom.
A rational expression is proper if the degree of the numerator is less than the degree of the denominator and improper otherwise. F 1 C is compact for all compact sets C C. You can find oblique asymptotes using polynomial division where the quotient is.
For example look at these three rational expressions. The function has the form. Qx will be the.
And its proper and proper is going to mean that the degree of the denominator is larger than the degree of the numerator than this graph. A rational function Rx pxqx in lowest terms will have a vertical asymptote x r if x - r is a factor of the denominator q. A linear fractional function is another example of a rational function.
A rational function will be zero at a particular value of x only if the numerator is zero at that x and the denominator isnt zero at that x. Any rational function can be written as the sum of a polynomial and a proper rational function. For rational functions this may seem like a mess to deal with.
Then fxgx is called a proper rational function. If degree of fx is greater than or equal to degree of gx then frac fx gx is called an improper rational function. F z p z q z for complex polynomials p z and q z such that f.
What is a Proper Rational Function. If this condition is not satisfied we perform long division until the residue polynomial is of degree. If degree of fx is less than degree of gxthen is called a proper rational function.
If the rational function is not proper if the degree of the numerator is equal to or larger than the degree of the denominator you can use polynomial division to convert the rational function into a polynomial plus a proper rational function. That is if r is a zero of the denominator of a rational function Rx pxqx in lowest terms then R will have the vertical asymptote x r. A proper rational function is a ratio of functions where the degree of the numerator the top number in a fraction is less than the degree of the denominator the bottom number.
Arrow_forward Determine whether each of the following statements is true or false and explain why. If a rational function is proper then y0 is a horizontal asymptote. Otherwise it is called improper.
C A C be analytic and proper where A is a finite point set in C. A vertical line that a graph approaches but never crosses. F x x2 5x 6 f x x 2 - 5 x 6.
A large mixing tank currently contains 100 gallons of water into which 5 pounds of sugar have been mixed. If in equation 1 n m m 0 then the rational function is said to be proper. This question does not show any research effort.

7 4 Integration Of Rational Functions By Partial Fractions Techniques Of Integration In This Section We Will Learn How To Integrate Rational Functions Ppt Download

Partial Fractions Definition Formula Decomposition Examples
Matematicas Visuales Rational Functions 1 Linear Rational Functions

Partial Fraction Method For Rational Functions

How To Determine The End Behavior Of A Rational Function Algebra Study Com
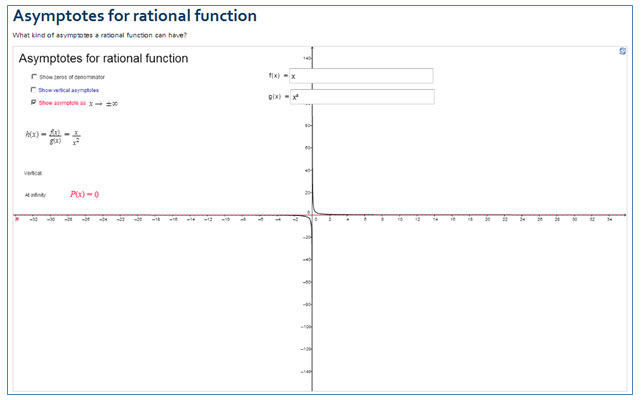
Rational Functions Predicting The Effects Of Parameter Changes Texas Gateway

Rational Functions Algebra And Trigonometry

2 6 Rational Functions Ppt Download
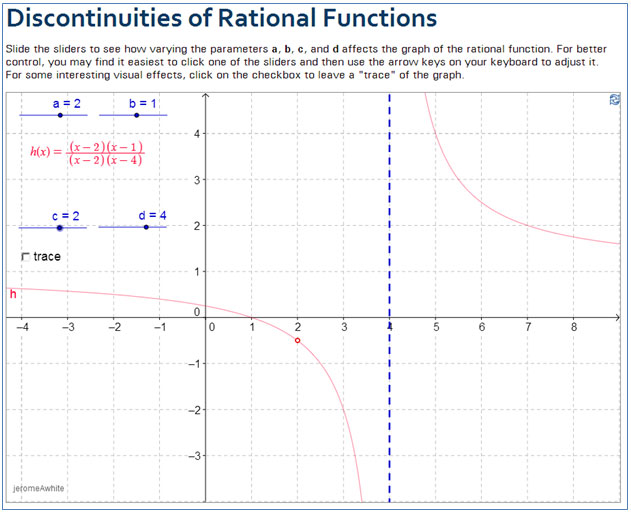
Rational Functions Predicting The Effects Of Parameter Changes Texas Gateway

Rational Function Graph Domain Range Asymptotes

Solved Graph The Rational Function X 3 63 1 X 3 Chegg Com

Solved 38 Let F And G Be Differentiable Functions Such That Chegg Com

Expressions Of Rational Functions Video Lesson Transcript Study Com

Partial Fractions A Plus Topper

End Behavior Of Rational Functions Video Khan Academy
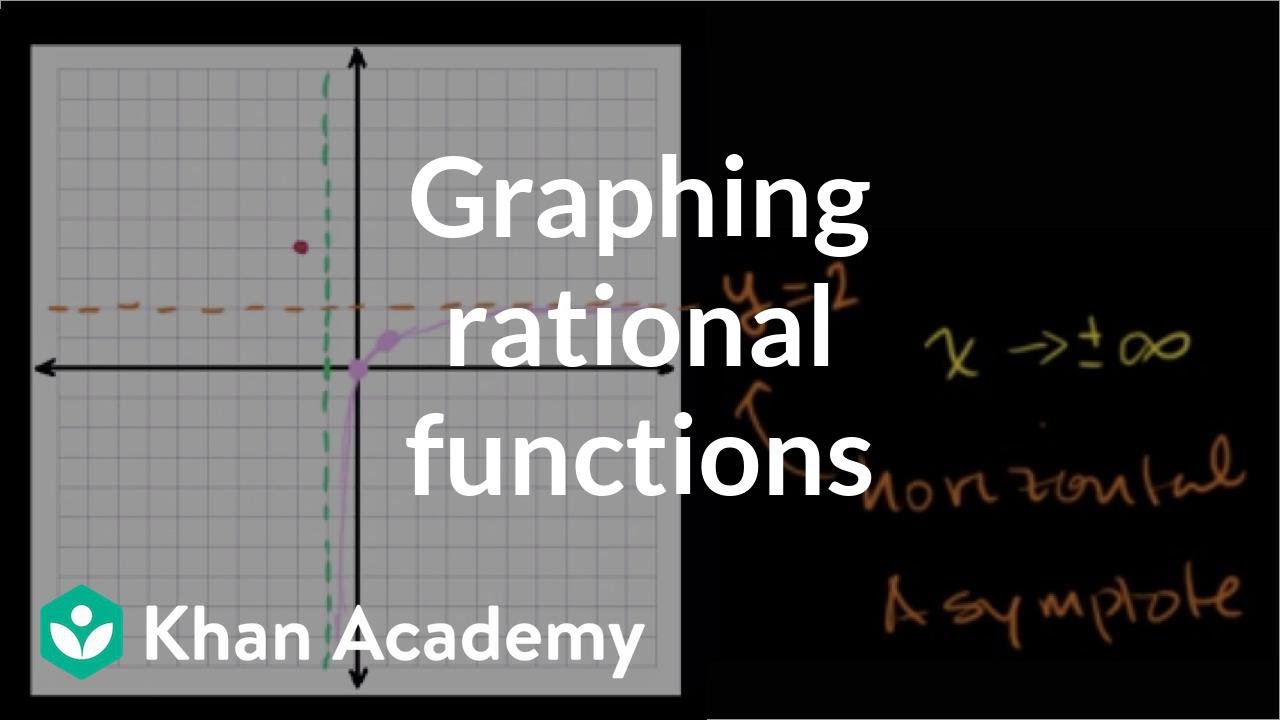
Graphing Rational Functions 2 Video Khan Academy

Partial Fraction Method For Rational Functions
Matematicas Visuales Rational Functions 1 Linear Rational Functions

Comments
Post a Comment